Guild of Project Controls: Compendium | Roles | Assessment | Certifications | Membership

Tips on using this forum..

(1) Explain your problem, don't simply post "This isn't working". What were you doing when you faced the problem? What have you tried to resolve - did you look for a solution using "Search" ? Has it happened just once or several times?

(2) It's also good to get feedback when a solution is found, return to the original post to explain how it was resolved so that more people can also use the results.

Critical Path Quiz answers

No replies
Tue, 2011-07-05 13:41
Stephen Devaux
User offline. Last seen 18 weeks 51 min ago. Offline
Joined: 23 Mar 2005
Posts: 667
Groups: Content Moderators

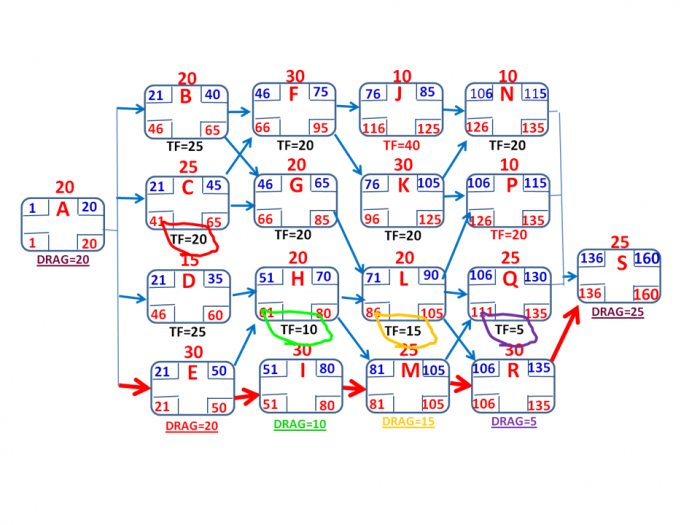
So here are the answers to the quiz, along with an explanation of how to compute critical path drag in a simple (all FS) network:

  1. Which activity or activities has/have the most total float, and how much? J has TF = 40
  2. Which activity or activities has/have EXACTLY fifteen units of free float? Activities D & L have exactly 15 units of free float.
  3. How many units of time is each critical path activity ADDING to the total project duration of 160 units (i.e., what is the drag of each activity)?

Drag is ONLY on critical path activities, and in a network with ONLY FS relationships, it can easily be computed as follows:

  1. If an activity has NOTHING ELSE IN PARALLEL (i.e., no other activity is on a completely different path), an activity's drag is equal to its duration.
  2. If an activity has other things in parallel (i.e., other activities that are not on the same path as the critical path activity), the drag of the critical path activity will be whichever is LESS: its duration or the total float of the parallel activity that has the LEAST total float.

To show the answers to the exercise in diagram form:

563
planningplanetexer1answer_upload.png

Top